Arduino Auto Ranging Ohmmeter, Part 1

An Arduino auto ranging ohmmeter is easy to implement using an Arduino Uno or other Arduino development boards. And depending on the implementation, it can rival the accuracy of commercial digital ohmmeters available in the market.

To better appreciate an auto ranging Arduino ohmmeter, let us first create a simple ohmmeter using an Arduino Uno development board. After studying the underlying theory behind its operation, we will assemble a more accurate, full-pledged auto ranging ohmmeter.

The Simple Arduino Ohmmeter

A simple Arduino ohmmeter schematic diagram is shown below. It uses an Arduino Uno development board and a 10kΩ reference resistor (R_ref) in series with the resistor being tested (R_x).

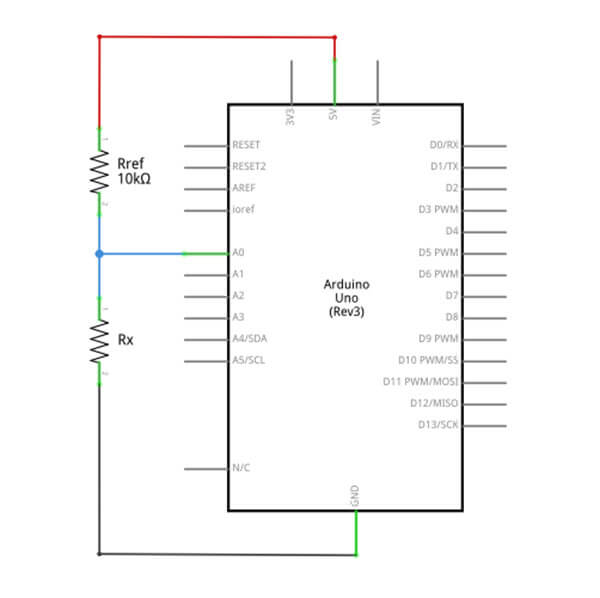
Schematic diagram of a simple arduino ohmmeter, the basis for an arduino auto ranging ohmmeter — Figure 1 – Simple Arduino Ohmmeter Schematic Diagram

The following Arduino IDE sketch will display the value of the unknown resistor R_x on the Arduino IDE’s serial monitor.

#define Rref 10000.0
void setup() {
Serial.begin(9600);
}
void loop()
{
uint16_t x = analogRead(A0);
float Rx = Rref * x/(1024 - x);
Serial.println(Rx);
delay(2000);
}

#define Rref 10000.0

void setup() {

Serial.begin(9600);

}

void loop()

{

uint16_t x = analogRead(A0);

float Rx = Rref * x/(1024 - x);

Serial.println(Rx);

delay(2000);

}

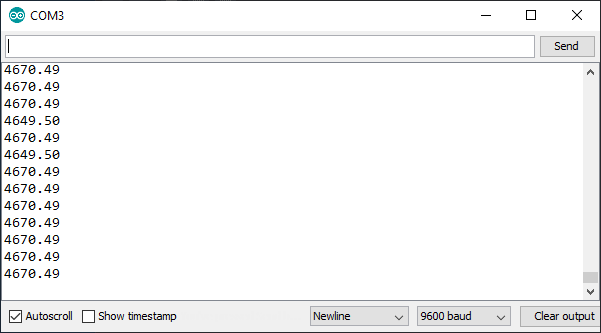
Here is a screenshot of the output of the sketch shown above. A resistor with a value of 4.7kΩ and a tolerance of 1% was used as R_x. The output shows a value of 4.670kΩ. However, it sometimes fluctuates to 4.649kΩ. The measured value looks close enough to the actual value of the resistor. Considering that a 1% tolerance is equal to 47Ω, we expect to get a value between 4.653kΩ and 4.747kΩ.

Screenshot of the serial monitor output of the simple arduino ohmmeter showing the measured resistance of a 4.7k ohms resistor — Figure 2 – Serial Monitor Output

Prelude to Arduino Auto Ranging Ohmmeter

How is resistance measured?

In an Arduino ohmmeter, the unknown resistance of a resistor is measured indirectly using Ohm’s Law.

The Current (I) flowing into a circuit is equal to the impressed Voltage (V) divided by the circuit Resistance (R).
Ohm’s Law

Image explaining the Ohm's law which is used in implementing an arduino auto ranging ohmmeter — Figure 3 – Ohm’s Law

$\fn_jvn {\color{Blue} \textup I=\frac{\textup V}{\textup R}}\qquad\qquad \textup {Ohm's Law}$

Using the above equation, if we know the voltage (V) across the resistor and the current (I) flowing through it, we can calculate its resistance value.

The voltage (V) across the resistor is easily measured by connecting it to the ADC (Analog to Digital Converter) pin of an Arduino development board. But we need a way to calculate the Current (I) flowing thru it so we can compute the Resistance R.

The Voltage Divider Circuit – Computing the Current (I)

There is a technique used to compute the current (I) thru an unknown resistor. The technique involves placing another resistor with a known value in series with the unknown resistor. The resulting circuit is known as a Voltage Divider Circuit. Please see Figure 4 below.

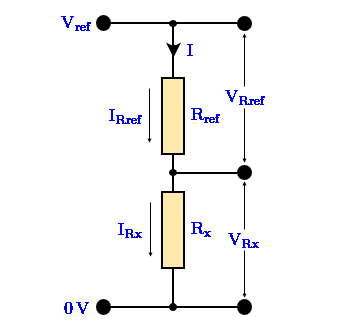
A diagram of a voltage divider circuit used in Arduino auto ranging ohmmeter — Figure 4 – Voltage Divider Circuit

In the voltage divider circuit above, R_ref is the resistor of a known value and R_x is the unknown resistor being measured. V_Rx will be read and measured by an ADC, hence, let us assume that this is a known voltage.

The input voltage V_ref is divided between the two resistors in series, R_ref and R_x. Therefore,

$\fn_jvn {\color{Blue} \textup V_{\textup {ref}}=\textup V_{\textup {Rref}}+\textup V_{\textup {Rx}}}\qquad\qquad \textup{\textsc{\scriptsize(Equation 0.1)}}$

and the voltage V_Rref across the known resistor R_ref is,

$\fn_jvn {\color{Blue} \textup V_{\textup {Rref}}=\textup V_{\textup {ref}}-\textup V_{\textup {Rx}}}\qquad\qquad \textup{\textsc{\scriptsize(Equation 0.2)}}$

Since R_ref is of a known resistance and we already know the voltage across it, we can now compute the value of I_Rref, the current passing thru it.

$\fn_jvn {\color{Blue}\textup I_{\textup {Rref}}=\frac{\textup V_{\textup {Rref}}}{\textup R_\textup {ref}}=\frac{\textup V_{\textup {ref}}-\textup V_{\textup {Rx}}}{\textup R_{\textup {ref}}}}\qquad\qquad \textup{\textsc{\scriptsize(Equation 0.3)}}$

The current I_Rref is the same current flowing thru the unknown resistor R_x. So, it follows that,

$\fn_jvn {\color{Blue}\textup I_{\textup {Rx}}=\textup I_{\textup {Rref}}=\frac{\textup V_{\textup {ref}}-\textup V_{\textup {Rx}}}{\textup R_{\textup {ref}}}}\qquad\qquad \textup{\textsc{\scriptsize(Equation 0.4)}}$

Finally, to compute the resistance of the unknown resistor, R_x, we substitute Equation 0.4 in the resistance formula below.

$\fn_jvn {\color{Blue}\textup R_{\textup {x}}=\frac{\textup V_{\textup {Rx}}}{\textup I_\textup {Rx}}=\frac{\textup V_{\textup {Rx}}}{\frac{\textup V_{\textup {ref}}-\textup V_{\textup {Rx}}}{\textup R_{\textup {ref}}}}}\qquad\qquad \textup{\textsc{\scriptsize(Equation 0.5)}}$

Rearranging Equation 0.5, we get the final equation for computing R_x.

$\dpi{120} \fn_jvn {\color{Blue}\textup R_{\textup {\textup x}}=\frac{\textup R_{\textup {ref}}*\textup V_{\textup {Rx}}}{{\textup V_{\textup {ref}}-\textup V_{\textup {Rx}}}}}\qquad\qquad \textup{\textsc{\scriptsize(Equation 1)}}$

Analog to Digital Converter – Measuring Voltage Across the Resistor

The voltage across the resistor being measured is fed to the ADC of an Arduino development board. Arduino Uno’s ADC has a resolution of 10 bits or 2¹⁰, which is equal to 1024. This means that the reference voltage for the ADC is divided by 1024. Representing the ADC output reading with the variable x, V_Rx can be computed using the formula:

$\dpi{120} \fn_jvn {\color{Blue}\textup V_{\textup {\textup {Rx}}}=\frac{\textup V_{\textup {ref}}}{1024}*\textup x}\qquad\qquad \textup{\textsc{\scriptsize(Equation 2.0)}}$

Also, given the value of V_Rx, which is the input to the ADC, we can find the value of x by using the formula:

$\dpi{120} \fn_jvn {\color{Blue}\textup x=\frac{1024}{\textup V_{\textup {ref}}}*\textup V_{\textup {Rx}}}\qquad\qquad \textup{\textsc{\scriptsize(Equation 2.1)}}$

Caveat:
The Arduino’s Due, Zero and MKR Family boards have 12-bit ADC capabilities but are by default set to 10-bit resolution. If they are run in 12-bit resolution by calling analogReadResolution(12), the constant 1024 must be replaced with 4096.
See Reference on analogReadResolution()

Using Equation 1 and Equation 2.0 as mentioned above, we can compute the value of the unknown resistor R_x if we have the ADC output reading x.

In an Arduino IDE sketch, we may use the following code to compute the value of R_x:

#define Rref 10000.0
void setup() {
uint16_t x = analogRead(A0);
float Vrx = x * 5.0/1024  //compute voltage across resistor  
float Rx = Rref * Vrx /(5.0-Vrx);  //compute resistance

#define Rref 10000.0

void setup() {

uint16_t x = analogRead(A0);

float Vrx = x * 5.0/1024 //compute voltage across resistor

float Rx = Rref * Vrx /(5.0-Vrx); //compute resistance

Computing Rx as a Function of x

The Equation 1 above for computing the value of the unknown resistor R_x is based on a pre-computed value of V_Rx. Actually there is a more simple formula for figuring out the value of R_x. The output value x of the ADC can be used to directly compute R_x. The formula is:

$\dpi{120} \fn_jvn {\color{Blue}\textup R_{\textup {\textup x}}=\frac{\textup R_{\textup {ref}}*\textup x}{{1024-\textup x}}}\qquad\qquad \textup{\textsc{\scriptsize(Equation 3)}}$

Notice the similarity of Equation 1 & Equation 3. The voltages, V_ref and V_Rx, were simply replaced with their equivalent ADC values.

Let’s do a little exercise. We’ll try to prove that Equation 1 and Equation 3 are indeed equal to each other.

First, using the voltage divider circuit in Figure 2, the value of the voltage V_Rx (again using Ohm’s Law) is,

$\fn_jvn {\color{Blue}\textup V_{\textup {Rx}}=\textup I_{\textup Rx}*\textup R_{\textup {x}}=\frac{\textup V_{\textup {ref}}}{\textup R_{\textup{ref}}+\textup R_{\textup x}}*\textup R_{\textup x}}\qquad\qquad \textup{\textsc{\scriptsize(Equation 4)}}$

V_Rx is fed into the ADC, so we can use Equation 2,

$\fn_jvn {\color{Blue}\textup V_{\textup {\textup {Rx}}}=\frac{\textup V_{\textup {ref}}}{1024}*\textup x}\qquad\qquad \textup{\textsc{\scriptsize(Equation 2.0)}}$

Equating Equation 4 and Equation 2.0, we have,

$\fn_jvn {\color{Blue}\frac{\textup V_{\textup {ref}}}{\textup R_{\textup{ref}}+\textup R_{\textup x}}*\textup R_{\textup x}=\frac{\textup V_{\textup{ref}}}{1024}*\textup x}$

Using the cross multiplication method,

$\fn_jvn {\color{Blue}\textup V_{\textup {ref}}*\textup R_{\textup{x}}*1024=(\textup R_{\textup {ref}}+\textup R_\textup x)*\textup V_{\textup {ref}}*\textup x}$

Move V_ref and 1024 to the right side of the equation.

$\fn_jvn {\color{Blue}\textup R_{\textup{x}}=\frac{(\textup R_{\textup {ref}}+\textup R_\textup x)*\textup V_{\textup {ref}}*\textup x}{\textup V_{\textup {ref}}*1024}}$

Cancel out V_ref.

$\fn_jvn {\color{Blue}\textup R_{\textup x}=\frac{\textup x*(\textup R_{\textup {ref}}+\textup R_\textup x)}{1024}}$

We need to remove the variable R_x that is on the right side of the equation. Multiply the terms of the numerator and then separate the two terms.

$\fn_jvn {\color{Blue}\textup R_{\textup x}=\frac{\textup x*\textup R_{\textup {ref}}}{1024}+\frac{\textup x*\textup R_\textup x}{1024}}$

Move the second term containing the variable R_x to the left side of the equation.

$\fn_jvn {\color{Blue}\textup R_{\textup x}-\frac{\textup x*\textup R_\textup x}{1024}=\frac{\textup x*\textup R_\textup {ref}}{1024}}$

Factor out R_x.

$\fn_jvn {\color{Blue}\textup R_{\textup x}(1-\frac{\textup x}{1024})=\frac{\textup x*\textup R_\textup {ref}}{1024}}$

Multiplying both sides of the equation with 1024, we get,

$\fn_jvn {\color{Blue}\textup R_{\textup x}(1024-\textup x)=\textup x*\textup R_\textup {ref}}$

Finally move the term in the parenthesis to the right side of the equation.

$\fn_jvn {\color{Blue}\textup R_\textup x=\frac{\textup R_\textup {ref}*\textup x}{{1024-\textup x}}}\qquad\qquad \textup{\textsc{\scriptsize(Equation 3)}}$

This shows that we can directly use the ADC output x, which is the value from the analogRead() function, to compute the value of R_x without the need to compute the value of V_Rx.

The Ohmmeter Accuracy

Referring to Figure 4 above, let’s compute V_Rx in terms of the two series resistors.

$\dpi{120} \fn_jvn {\color{Blue}\textup V_{\textup {Rx}}=\textup I_{\textup Rx}*\textup R_{\textup {x}}=\frac{\textup V_{\textup {ref}}*\textup R_\textup x}{\textup R_{\textup{ref}}+\textup R_\textup x}}\qquad\qquad \textup{\textsc{\scriptsize(Equation 4)}}$

Now, assume the following resistor values: R_ref = 10KΩ and R_x = 10KΩ. Let’s compute V_Rx using Equation 4.

$\fn_jvn {\color{Blue}\textup V_{\textup {Rx}}=\frac {5\textup V*10\textup k\Omega}{10\textup k\Omega+10\textup k\Omega}=2.5\textup V}$

Compute x using Equation 2.1.

$\fn_jvn {\color{Blue}\textup x=\frac{1024}{\textup V_{\textup {ref}}}*\textup V_{\textup {Rx}}}$

$\fn_jvn {\color{Blue}\textup x=\frac{1024*2.5\textup V}{5\textup V}=512}$

Let us do the same computation for the values of R_ref = 10KΩ and R_x = 1KΩ.

$\fn_jvn {\color{Blue}\textup V_{\textup {Rx}}=\frac {5\textup V*1\textup k\Omega}{10\textup k\Omega+1\textup k\Omega}=\frac{5\textup V}{11}=0.4545\textup V}$

$\fn_jvn {\color{Blue}\textup x=\frac{1024*0.4545\textup V}{5\textup V}=93}$

Again, compute for R_ref = 10KΩ and R_x = 100Ω.

$\fn_jvn {\color{Blue}\textup V_{\textup {Rx}}=\frac {5\textup V*100\Omega}{10\textup k\Omega+100\Omega}=\frac{500\textup V}{10,100}=0.0495\textup V}$

$\fn_jvn {\color{Blue}\textup x=\frac{1024*0.0495\textup V}{5\textup V}=10}$

Using the three (3) computed ADC values, compute R_x using Equation 3.

$\fn_jvn {\color{Blue}\textup R_{\textup {\textup x}}=\frac{\textup R_{\textup {ref}}*\textup x}{{1024-\textup x}}}\qquad\qquad \textup{\textsc{\scriptsize(Equation 3)}}$

$\fn_jvn {\color{Blue}\textup R_{\textup {\textup x}}=\frac{10\textup k\Omega*512}{{1024-\textup 512}}=\frac{5120\textup k\Omega}{512}=10\textup k\Omega}$

$\fn_jvn {\color{Blue}\textup R_{\textup {\textup x}}=\frac{10\textup k\Omega*93}{{1024-\textup 93}}=\frac{930\textup k\Omega}{931}=0.9989\textup k\Omega}$

$\fn_jvn {\color{Blue}\textup R_{\textup {\textup x}}=\frac{10\textup k\Omega*10}{{1024-\textup 10}}=\frac{100\textup k\Omega}{1014}=98.6\Omega}$

Below is a table of the above computations.

R_ref	R_x (Actual)	V_Rx	ADC (x)	R_x (Computed)
10kΩ	10kΩ	2.5V	512	10.00kΩ
10kΩ	1kΩ	0.4545V	93	0.9989kΩ
10kΩ	100Ω	0.0495V	10	98.6Ω

If you compare column 2, Rx (Actual) and column 5, Rx (Computed) of the table shown above, you will notice that there are discrepancies between the actual R_x values and the computed R_x values of row 2 and row 3. Only the first row has the exact value of the computed R_x value. Also, take note that row 2 has a lower discrepancy compared to row 3.

To clearly see the problem, let us take a second set of computations. This time, instead of a 10kΩ R_ref, let’s use a value of 1kΩ for R_ref.

Rref = 1kΩ and Rx = 10kΩ

$\fn_jvn {\color{Blue}\textup V_{\textup {Rx}}=\frac {5\textup V*10\textup k\Omega}{1\textup k\Omega+10\textup k\Omega}=\frac{50\textup V}{11}=4.545\textup V}$

$\fn_jvn {\color{Blue}\textup x=\frac{1024*4.545\textup V}{5\textup V}=931}$

$\fn_jvn {\color{Blue}\textup R_{\textup {\textup x}}=\frac{1\textup k\Omega*931}{{1024-931}}=\frac{931\textup k\Omega}{93}=10.01\textup k\Omega}$

====================================

Rref = 1kΩ and Rx = 1kΩ

$\fn_jvn {\color{Blue}\textup V_{\textup {Rx}}=\frac {5\textup V*1\textup k\Omega}{1\textup k\Omega+1\textup k\Omega}=\frac{5\textup V}{2}=2.5\textup V}$

$\fn_jvn {\color{Blue}\textup x=\frac{1024*2.5\textup V}{5\textup V}=512}$

$\fn_jvn {\color{Blue}\textup R_{\textup {\textup x}}=\frac{1\textup k\Omega*512}{{1024-512}}=\frac{512\textup k\Omega}{512}=1\textup k\Omega}$

====================================

Rref = 1kΩ and Rx = 100Ω

$\fn_jvn {\color{Blue}\textup V_{\textup {Rx}}=\frac {5\textup V*100\Omega}{1\textup k\Omega+100\Omega}=\frac{500\textup V}{1100}=0.4545\textup V}$

$\fn_jvn {\color{Blue}\textup x=\frac{1024*0.4545\textup V}{5\textup V}=93}$

$\fn_jvn {\color{Blue}\textup R_{\textup {\textup x}}=\frac{1\textup k\Omega*93}{{1024-93}}=\frac{93\textup k\Omega}{931}=99.89\Omega}$

Here is the table for the second set of computations.

R_ref	R_x (Actual)	V_Rx	ADC (x)	R_x (Computed)
1kΩ	10kΩ	4.545V	931	10.01K
1kΩ	1kΩ	2.5V	512	1.00K
1kΩ	100Ω	0.4545V	93	99.89 Ohms

Studying the two tables will highlight the facts about the voltage divider circuit being used to measure the resistance of the unknown resistor R_x.

The most accurate measurement of the value of R_x occurs when R_x and R_ref are equal.
The higher the difference of the values of R_x and R_ref, the less accurate the measurement will be.

To reduce the error in the measurement of resistance, a solution is to use different values for R_ref. It can be implemented by manually switching reference resistors from a bank of resistors during a measurement.

Or better yet, automatically select and switch the proper value of R_ref electronically, and controlled by software. That leads us to an Arduino auto ranging ohmmeter.

Arduino Auto Ranging Ohmmeter, Part 2

References on Arduino Auto Ranging Ohmmeter

Ohmmeter Using Arduino – circuitstoday.com – diode in series with reference resistors
Arduino Based Auto-Ranging Ohmmeter – simple-circuit.com – transistor switch
Resistomatic – an Arduino-based autoranging ohm-meter -blog.rareshool.com – simple resistor bank, no diodes, no transistors
Arduino Digital Multimeter
How accurate is an Arduino Ohmmeter?
Why ADC/1024 is correct, and ADC/1023 is just plain wrong!
Online Equation Writer